数量关系备考:平面路径
在平面几何中,我们常常会碰到与路径相关的问题,主要有三种表现形式:第一,对于给定的平面几何图形,如果已知起点和终点,按照指定的规则,求不同路径的数量;第二,对于给定的平面几何图形,要求走完每一段路,求最短路径;第三,计算平面图形中两点之间的最短距离。由于平面路径系列问题内容较多,计划分三次来给大家呈现,本次主要介绍第一类:
对于给定的平面几何图形,如果已知起点和终点,按照指定的规则,求不同路径的数量。一般通用的方式是逐点标数(本质为递推和数列)。具体方法:①确定起点和终点,在起点处标1;②确定运动方向(转化成上下左右)后转换角度,即每一点可能来的路径数;③由起点到终点(由近及远)逐级求和,每一个点的路径数等于可能到达它的点的路径数之和。理论比较抽象,我们通过几道例题一起来看一下:
【例1】小张从华兴园到软件公司上班要经过多条街道(软件公司在华兴园的东北方)。假如他只能向东或者向北行走,则他上班不同走法共有:
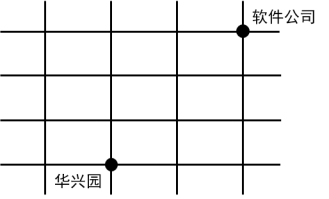
A.12种
B.15种
C.20种
D.10种
【答案】D
【解析】
第一步,已知了起点和终点,并确定了向东和向北的运动方向,求不同走法的总数,采用逐点标数法。先在起点处标1,并在正东和正北方向标1,如下图:

第二步,除起点外,任何一点只能从它的左边和下边过来(因为要求路程最短),分析之后,接着可以标记余下点的路径数。如下图:
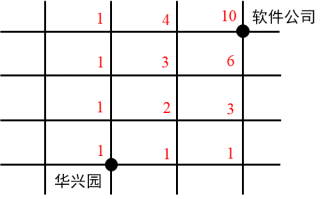
因此,选择D选项。
【例2】小赵从家出发去单位上班要经过多条街道(如图),假如他只能向西或向南行走。则他上班有多少种不同的走法?
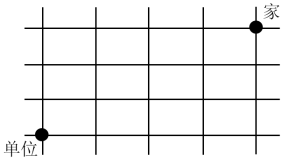
A.6
B.24
C.32
D.35
【答案】D
【解析】
第一步,已知了起点和终点,并确定了向西和向南的运动方向,求不同走法的总数,采用逐点标数法。先在起点处标1,并在正西和正南方向标1,如下图:

第二步,除起点外,任何一点只能从它的上边和右边过来(因为要求路程最短),分析之后,接着可以标记余下点的路径数。如下图:
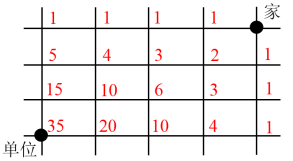
因此,选择D选项。

【例3】从A地到B地的道路如图所示,所有转弯均为直角,问如果要以最短距离从A地到达B地,有多少种不同的走法可以选择?

A.14
B.15
C.18
D.21
【答案】B
【解析】
第一步,已知了起点和终点,题干要求最短距离只能向右或向上行进,求不同走法的总数,采用逐点标数法。先在起点A处标1,并在正东和正北方向标1,如下图:

第二步,除起点外,任何一点只能从它的左边和下边过来(因为要求路程最短),分析之后,接着可以标记余下点的路径数。如下图:

因此,选择B选项。
【例4】A、B、C三地的地图如下图所示,其中A在C正北,B在C正东,连线处为道路。如要从A地到达B地,且途中只能向南、东和东南方向行进,有多少种不同的走法:

A.9
B.11
C.13
D.15
【答案】D
【解析】
第一步,已知了起点A和终点B,题干要求最短距离只能向南、向东或东南行进,求不同走法的总数,采用逐点标数法。先在起点A处标1,并在正南方向标1,如下图:

第二步,任何一点只能从它的上边、左边和左上方向过来(因为要求路程最短),分析明白之后,接着可以标记余下点的路径数。如下图:

因此,选择D选项。
对于平面几何中的路径类问题,即给定一个平面几何图形,已知起点和终点,按照指定的规则,求不同路径的数量的题目,虽然针对部分简单图形,排列组合可以使用,但并不是最常用的解法,我们最常用的解法是标数法(本质为递推和数列)。当然,需要各位同学把握好题目特征以及具体方法的操作步骤,只有熟练掌握才能灵活自如地运用。


时事热点练习题
点击查看>>公务员备考常识时事政治专项备考资料
共青团中央日前联合中央宣传部、国家发展改革委等17部门印发相关意见,指出到( )年,城市青年发展规划工作机制比较健全。
A. 2030
B. 2035
C. 2025
D. 2028
【答案】C【解析】本题考查时事热点。2022年4月2日电,共青团中央日前联合中央宣传部、国家发展改革委等17部门印发相关意见。指出到2025年,城市青年发展规划工作机制比较健全,青年优先发展理念得到社会广泛认同,青年发展型城市评价体系逐步建立并完善,城市青年发展政策更具体系化、更有普惠性,青年投身城市发展的主动性和贡献度明显提升。故本题正确答案为C项。
单选题
24. 2022年10月17日是第30个国际消除贫困日。现行标准下我国( )已如期全部脱贫。
A. 易地搬迁贫困人口 B. 西部地区贫困人口
C. 农村贫困人口 D. 深度特困人口
【答案】C【解析】本题考查时事热点。2022年10月17日是第30个国际消除贫困日。党的十八大以来,我国坚持把解决好“三农”问题作为重中之重,如期打赢脱贫攻坚战,历史性地解决了绝对贫困问题,工作重心由脱贫攻坚转入全面推进乡村振兴。现行标准下我国农村贫困人口已如期全部脱贫。故本题正确答案为C项。











