2021河南公务员考试每日一练解析(2月18日)
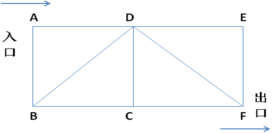
1、下图为某大厦走火通道逃离路线。某大厦集中所有的人员开展火灾逃生演习,从入口A点出发,要沿某几条线段才到出口F点。逃离中,同一个点或同一线段只能经过1次。假设所有逃离路线都是安全的,则不同的逃离路线最多有()种。
A.8
B.9
C.10
D.11
解析
第一步,本题考查其他杂题,用枚举法解题。
第二步,枚举逃离路线有:ABCF、ABCDF、ABCDEF、ABDCF、ABDF、ABDEF、ADEF、ADF、ADCF、ADBCF,共10条路线。
因此,选择C选项。

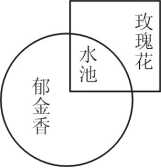
2、下图为某公园花展的规划图。其中,正方形面积的是玫瑰花展区,圆形面积的是郁金香花展区,且郁金花展区比玫瑰花展区多占地450平方米。那么,水池占地()平方米。
A.100
B.150
C.225
D.300
解析
解法一:
第一步,本题考查几何问题,属于平面几何类。

因此,选择B选项。
解法二:
第一步,本题考查几何问题,属于平面几何类。
第二步,设水池的占地面积为x,则正方形、圆形的面积分别为4x、7x,郁金香的占地面积为6x,玫瑰花的占地面积为3x。故6x-3x=450,解得x=150平方米。
因此,选择B选项。
3、已知自行车与摩托车的速度比是2∶3,摩托车与汽车的速度比是2∶5。已知汽车15分钟比自行车多走11公里,问自行车30分钟比摩托车少走多少公里?
A.2
B.4
C.6
D.8
解析
第一步,本题考查行程问题,属于基本行程类,用比例法解题。
第二步,根据两个速度比可得V自∶V摩=2∶3=4∶6,V摩∶V汽=2∶5=6∶15,则V自∶V摩∶V汽=4∶6∶15。
第三步,设自行车、摩托车、汽车的速度分别为4v、6v、15v。由汽车15分钟比自行车多走11公里,有15×(15v-4v)=11,即15v=1;自行车30分钟比摩托车少走30×(6v-4v)=60v=4(公里)。
因此,选择B选项。
4.(单选题)某轮船发生漏水事故,漏洞处不断地匀速进水,船员发现险情后立即开启抽水机向外抽水。已知每台抽水机每分钟抽水20立方米,若同时使用2台抽水机15分钟能把水抽完,若同时使用3台抽水机9分钟能把水抽完。当抽水机开始向外抽水时,该轮船已进水()立方米。
A.360
B.450
C.540
D.600
解析
第一步,本题考查牛吃草问题。
第二步,设轮船已进水y,每分钟漏水为x,根据题意有:y=(40-x)×15,y=(60-x)×9,解得y=450。
因此,选择B选项。
5.(单选题)清晨,爷爷、爸爸和小磊在同一条笔直跑道上朝同一方向匀速晨跑。某一时刻,爷爷在前,爸爸在中,小磊在后,且三人之间的间距正好相等。跑了12分钟后小磊追上了爸爸,又跑了6分钟后小磊追上了爷爷,则再过()分钟,爸爸可追上爷爷。
A.12
B.15
C.18
D.36
解析
第一步,本题考查行程问题,属于相遇追及类。

因此,选择C选项。
6、甲、乙、丙三村共建一项水利工程,原计划三村派出的劳动力之比为8∶5∶7,因丙村劳动力紧张,经协调,丙村少出的劳动力由甲、乙两村分担,相应的工钱由丙村承担。若甲、乙、丙三村派出的实际人数分别为84、52、24,丙村付给甲、乙两村的工钱共5.6万元,则丙村给甲村的工钱为:
A.2.1万元
B.2.8万元
C.3.5万元
D.4.2万元
解析
第一步,本题考查基础应用题。

因此,选择C选项。
7、参加某运动会的全体运动员在开幕式上恰好排成一个正方形,有两行两列的运动员离场后,运动员人数减少64人,则参加该运动会的运动员人数为:
A.225
B.256
C.289
D.324
解析
第一步,本题考查方阵问题。
第二步,设最初的正方形每行每列均有x人,由题意可列方程:2x+2×(x-2)=64,解得x=17,所以参加该运动会的运动员总人数为17×17=289(人)。
因此,选择C选项。
8、某单位欲将甲、乙、丙、丁4个大学生分配到3个不同的岗位实习,若每个岗位至少分到1名大学生,且甲、乙两人被分在同一岗位,则不同的分配方法共有:
A.6种
B.8种
C.9种
D.12种
解析
第一步,本题考查排列组合问题,属于方法技巧类。
![]()
第二步,由于甲、乙两人被分在同一岗位,则将甲乙捆绑在一起,相当于三个元素分配到3个岗位,有(种)分配方法。
因此,选择A选项。
9、用A、B、C三种不同型号的挖掘机完成一项土方工程,A型5台和B型4台一起挖2天正好完成;A型10台和C型12台一起挖1天正好完成;B型2台和C型3台一起挖4天正好完成。若先用A型1台工作5天,再用B型2台工作2天,最后用C型3台完成剩下的工程,则完成该项工程共需的天数为:
A.8
B.9
C.10
D.11
解析
第一步,本题考查工程问题,属于效率类。
第二步,设A、B、C三种挖掘机的效率分别为a、b、c。由题意可得(5a+4b)×2=(10a+12c)×1=(2b+3c)×4,解得a∶b∶c=12∶15∶10。
![]()
第三步,赋值A、B、C三种挖掘机的效率分别为12、15、10,则工程总量为(5×12+4×15)×2=240。现用1台A工作5天,再用2台B工作2天后,还剩余的工作量为240-12×5-2×15×2=120,则需要3台C再工作(天)完成。故完成该项工程共需的天数为5+2+4=11(天)。
因此,选择D选项。
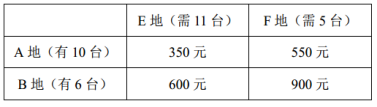
10、A、B两地分别有10台和6台型号相同的机器,准备配送到E、F两地,其中E地11台,F地5台,若每台机器从A到E和F的物流费用分别为350元和550元,从B到E和F的物流费用分别为600元和900元,则配送这16台机器的总物流费用最少为:
A.7850元
B.8100元
C.8400元
D.8700元
解析
第一步,本题考查经济利润问题,属于最值优化类。
第二步,列表分析,可得A→F比A→E每台费用高200元,而B→F比B→E每台费用高300元,所以要让B地的机器尽量配送到E地,6台机器的物流费用为600×6=3600(元),然后A地的10台机器配送给E地5台,给F地5台,物流费用为5×350+5×550=4500(元)。故配送这16台机器的总物流费用最少为3600+4500=8100(元)
因此,选择B选项。










